Contents

introduction

% s_GDSI_tutorial.m
%
%   A tutorial for generalized diffusion spectrum MRI (GDSI) reconstruction.
%
%   Source code:
%       https://github.com/qiyuantian/GDSI/blob/master/s_GDSI_tutorial.m
%
%   HTML file can be automatically generaged using command:
%       publish('s_GDSI_tutorial.m', 'html');
%
%   Reference:
%       [1] Tian Q, Yang G, Leuze C, Rokem A, Edlow BL, McNab JA, Generalized
%       Diffusion Spectrum Magnetic Resonance Imaging (GDSI) for Model-free
%       Reconstruction of the Ensemble Average Propagator. NeuroImage, 2019;
%       189: 497-515.
%
% (c) Qiyuan Tian, Stanford RSL

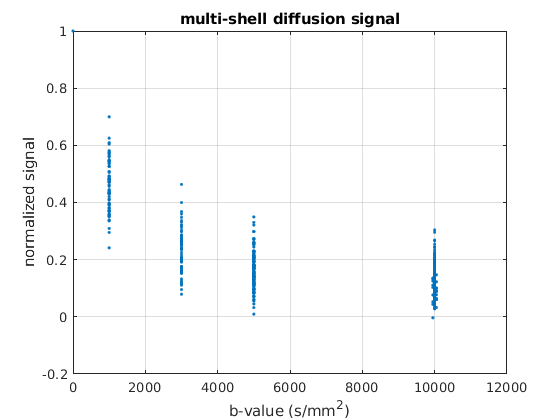
prepare diffusion data

% Load a single voxel from MGH-USC HCP data (pink box in Fig.10 in [1]),
% with 40xb=0, 64xb=1k, 64xb=3k, 128xb=5k, 256xb=10k
clear, clc, close all
load('data/multishell_vox.mat');

mask_b0 = bval == 0;
b0s = data(mask_b0); % b0 volumes
dwis = data(~mask_b0); % dwi volumes

data = [mean(b0s); dwis]; % average b0 volumes
data = data / mean(b0s); % normalize using b0
bval = [0; bval(~mask_b0)]; % new bval
bvec = [[0, 0, 0]; bvec(~mask_b0, :)]; % new bvec

% display data
figure
plot(bval, data, '.');
grid on;
title('multi-shell diffusion signal');
xlabel('b-value (s/mm^2)');
ylabel('normalized signal');

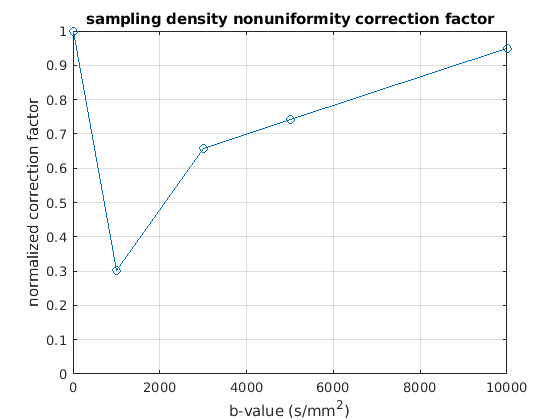
calculate q-space sampling density nonuniformity correction factor (Fig.4b in [1])

bval = bval(:); % column vector
disp('double check unique b values are:');
disp(unique(bval)); % note a +/- 50 variance at b=10k
bval_rnd = round(bval / 200) * 200; % round up bval

bval_uniq = unique(bval_rnd); % unique bval
count = zeros(size(bval_uniq)); % number of each bval
for ii = 1 : length(bval_uniq)
    count(ii) = sum(bval == bval_uniq(ii));
end

qval_uniq = sqrt(bval_uniq / max(bval_uniq)); % nomalize unique qval, q~sqrt(b)
qval_contour = (qval_uniq(1 : end-1) + qval_uniq(2 : end)) / 2; % middle contours
qval_contour = [qval_contour; 2 * qval_uniq(end) - qval_contour(end)]; % extrapolate one outer contour

qvol_shell = diff(qval_contour .^ 3); % qspace volume associated with each shell
qvol_shell = [qval_contour(1) .^ 3; qvol_shell]; % add in central sphere volume

qvol_shell = qvol_shell / qvol_shell(1); % normalize central sphere volume to 1
qvol_samp = qvol_shell ./ count; % qspace volume associated with a sample on a shell

qvol = zeros(size(bval)); % qspace volume for each sample (C in Eq.4 in [1])
for ii = 1 : length(bval_uniq)
    b = bval_uniq(ii);
    qvol(bval == b) = qvol_samp(ii);
end

% or can be simply computed using shelldens.m
% qvol = shelldens(bval, 200);

% display correction factor
figure
plot(bval_uniq, qvol_samp, '-o');
grid on;
ylim([0, 1]);
title('sampling density nonuniformity correction factor');
xlabel('b-value (s/mm^2)');
ylabel('normalized correction factor');

double check unique b values are:
           0
        1000
        3000
        5000
        9950
       10000
       10050

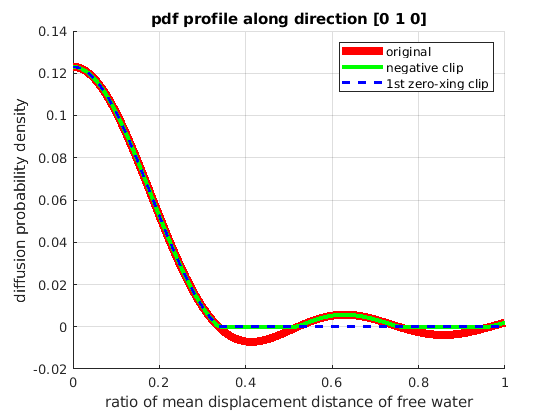
reconstruct 1D PDF profile along a specific direction (Fig.5f in [1])

nr = 100;
rs = linspace(0, 1, nr)'; % 100 distances btw [0, 1] of MDD of free water
pdf_dir = [0, 1, 0]; % A-P direction

rvec = repmat(pdf_dir, [nr, 1]) .* repmat(rs, [1, 3]); % 100 displacements along A-P direction
qvec = repmat(sqrt(6 * 0.0025 * bval), [1, 3]) .* bvec;
F = cos(rvec * qvec') / length(bval); % Fourier matrix, Eq.5 in [1]

pdf_1d = F * diag(qvol) * data; % Eq.4 in [1]

pdf_1d_clip = pdf_1d;
pdf_1d_clip(pdf_1d < 0) = 0; % clip negative pdf values to 0

pdf_1d_ringfree = pdf_1d;
ind_negative = find(pdf_1d < 0);
pdf_1d_ringfree(ind_negative(1):end) = 0; % set pdf values beyond 1st zero-crossing to 0

% display pdf profile
figure, hold all
plot(rs, pdf_1d, 'r', 'LineWidth', 6);
plot(rs, pdf_1d_clip, 'g', 'LineWidth', 3);
plot(rs, pdf_1d_ringfree, 'b--', 'LineWidth', 2);
grid on;
legend('original', 'negative clip', '1st zero-xing clip')
title(['pdf profile along direction ' mat2str(pdf_dir)]);
xlabel('ratio of mean displacement distance of free water');
ylabel('diffusion probability density');

reconstruct 3D PDF contour at a specific distance (Fig.5j in [1])

[x, y ,z] = sphere(64); % sphere object
fvc = surf2patch(x, y, z, z); % face, vertex and color data
pdf_dirs = fvc.vertices; % directions on a sphere

figure
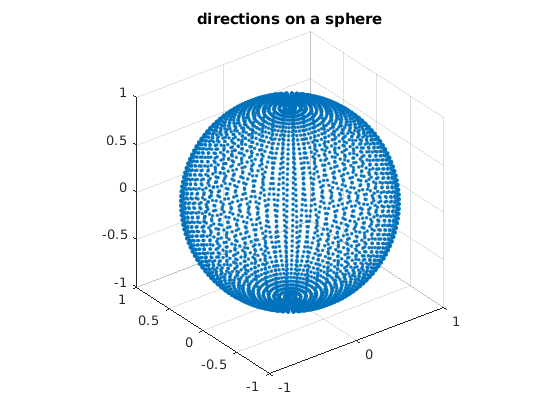
plot3(pdf_dirs(:,1),pdf_dirs(:,2),pdf_dirs(:,3), '.');
axis equal
grid on;
title('directions on a sphere');

r0 = 0.5; % 0.5 of MDD of free water
rvec = r0 * pdf_dirs;
qvec = repmat(sqrt(6 * 0.0025 * bval), [1, 3]) .* bvec;
F = cos(rvec * qvec') / length(bval);  % Fourier matrix, Eq.5 in [1]

pdf_3d = F * diag(qvol) * data;

pdf_3d_clip = pdf_3d;
pdf_3d_clip(pdf_3d < 0) = 0; % clip negative pdf values to 0

pdf_actor = fvc;
pdf_actor.vertices = fvc.vertices .* repmat(pdf_3d, [1, 3]); % scale radial distance
pdf_actor.facevertexcdata = pdf_3d; % change color data to represent pdf values

% display pdf contour
figure
h = patch(pdf_actor);
view(0, 0)
lighting gouraud
shading faceted
camlight
set(h, 'EdgeColor', 'none');

colormap;
colorbar;
caxis([min(pdf_3d(:)), max(pdf_3d(:))]);

axis equal, axis off, axis tight
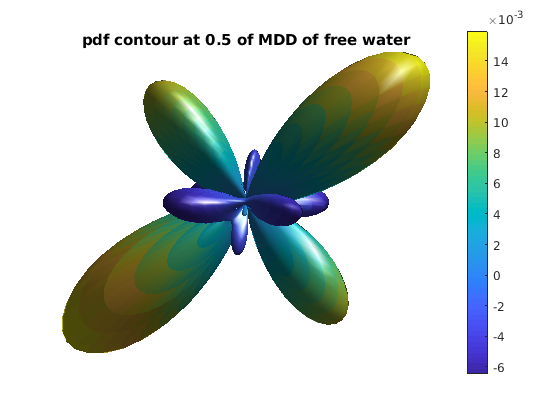
title(['pdf contour at ' num2str(r0) ' of MDD of free water']);

% display positive pdf contour
pdf_actor = fvc;
pdf_actor.vertices = fvc.vertices .* repmat(pdf_3d_clip, [1, 3]); % scale radial distance
pdf_actor.facevertexcdata = pdf_3d_clip; % change color data to represent pdf values

figure
h = patch(pdf_actor);
view(0, 0)
lighting gouraud
shading faceted
camlight
set(h, 'EdgeColor', 'none');

colormap;
colorbar;
caxis([min(pdf_3d(:)), max(pdf_3d(:))]);

axis equal, axis off, axis tight
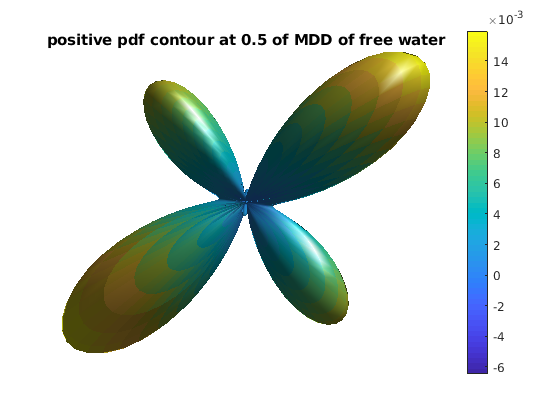
title(['positive pdf contour at ' num2str(r0) ' of MDD of free water']);

reconstruct ODF using direct approach (Fig.9 in [1])

[x, y ,z] = sphere(64); % sphere object
fvc = surf2patch(x, y, z, z); % face, vertex and color data
odf_dirs = fvc.vertices; % directions on a sphere

nr = 100;
rs = linspace(0, 0.8, nr)'; % 100 distances btw [0, 0.8] of MDD of free water
R = zeros(length(odf_dirs), length(data));
qvec = repmat(sqrt(6 * 0.0025 * bval), [1, 3]) .* bvec;
for ii = 1 : nr
    r = rs(ii);
    rvec = r * odf_dirs;
    F = cos(rvec * qvec') / length(bval) * (r^2);
    R = R + F; % odf recon matrix R, Eq.9 in [1]
end

odf_direct = R * diag(qvol) * data; % Eq.9 in [1]
% odf_direct(odf_direct < 0) = 0; % clip negative values
% odf_direct = odf_direct - min(odf_direct(:)); % remove offset

% display odf
odf_actor = fvc;
odf_actor.vertices = fvc.vertices .* repmat(odf_direct, [1, 3]); % scale radial distance
odf_actor.facevertexcdata = odf_direct; % change color data to represent pdf values

figure
h = patch(odf_actor);
view(0, 0)
lighting gouraud
shading faceted
camlight
set(h, 'EdgeColor', 'none');

colormap;
colorbar;
caxis([min(odf_direct(:)), max(odf_direct(:))]);

axis equal, axis off, axis tight
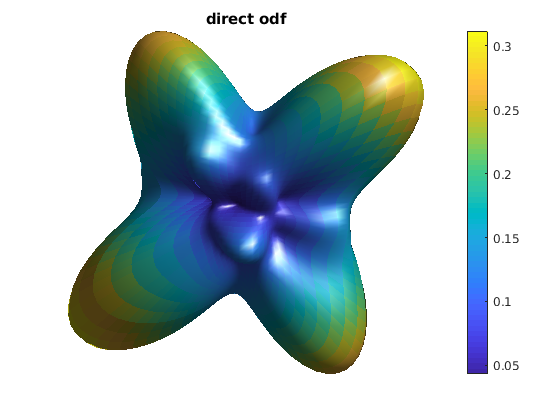
title('direct odf');

% display component odf at single shell
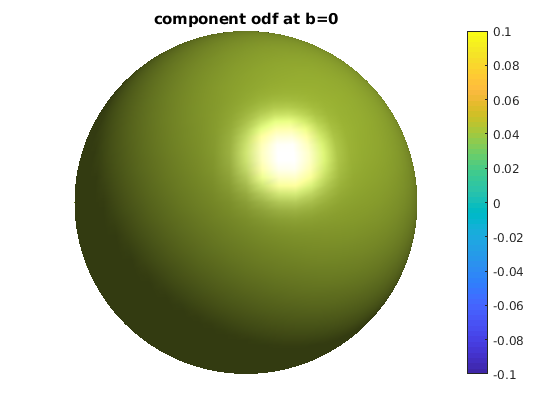
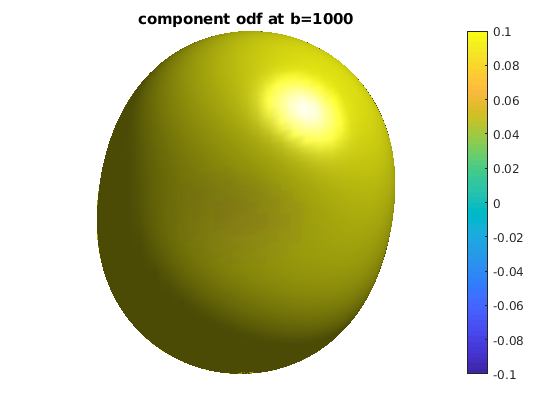
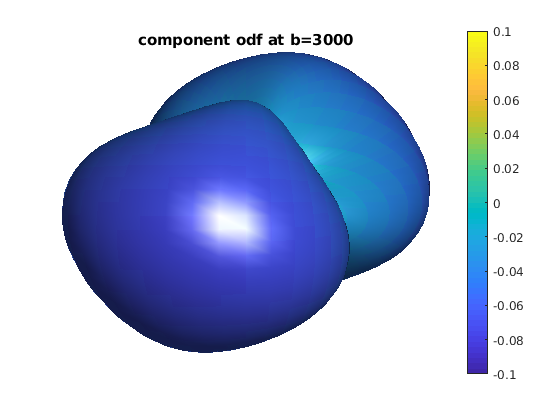
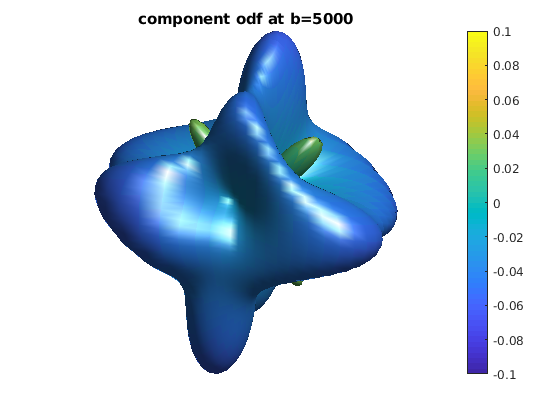
for ii = 1 : length(bval_uniq)
    b = bval_uniq(ii);
    data_shell = data;
    data_shell(bval_rnd ~= b) = 0;
    odf_shell = R * diag(qvol) * data_shell;

    odf_actor = fvc;
    odf_actor.vertices = fvc.vertices .* repmat(odf_shell, [1, 3]); % scale radial distance
    odf_actor.facevertexcdata = odf_shell; % change color data to represent pdf values

    figure
    h = patch(odf_actor);
    view(0, 0)
    lighting gouraud
    shading faceted
    camlight
    set(h, 'EdgeColor', 'none');

    colormap;
    colorbar;
    caxis([-0.1, 0.1]);

    axis equal, axis off, axis tight
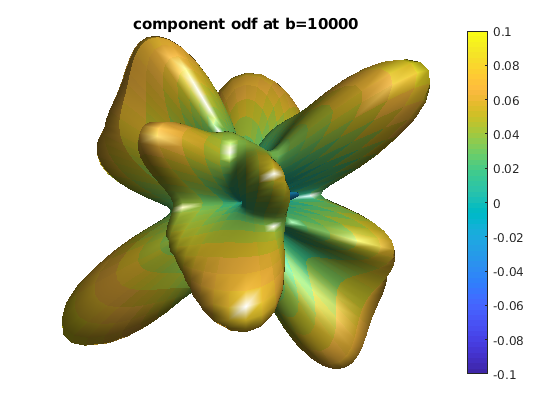
    title(['component odf at b=' num2str(b)]);
end

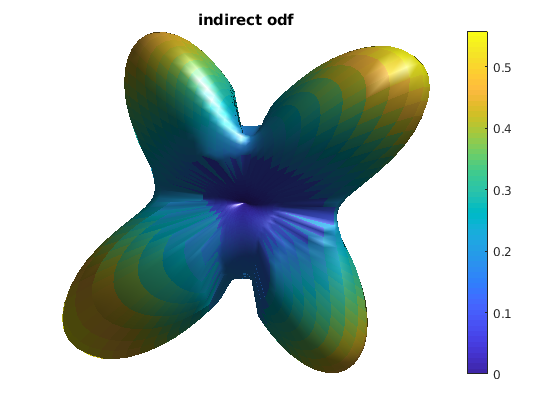
reconstruct ODF using indirect approach (Fig.9 in [1])

[x, y ,z] = sphere(64); % sphere object
fvc = surf2patch(x, y, z, z); % face, vertex and color data
odf_dirs = fvc.vertices; % directions on a sphere

nr = 100;
rs = linspace(0, 0.8, nr)'; % 100 distances btw [0, 1] of MDD of free water

qvec = repmat(sqrt(6 * 0.0025 * bval), [1, 3]) .* bvec;
pdf = zeros(length(odf_dirs), nr);

for ii = 1 : length(odf_dirs)
    pdf_dir = odf_dirs(ii, :);

    rvec = repmat(pdf_dir, [nr, 1]) .* repmat(rs, [1, 3]);
    F = cos(rvec * qvec') / length(bval); % Fourier matrix, Eq.5 in [1]

    pdf_1d = F * diag(qvol) * data; % Eq.4 in [1]
    ind_negative = find(pdf_1d < 0);
    if ~isempty(ind_negative)
        pdf_1d(ind_negative(1):end) = 0; % set pdf values beyond 1st zero-crossing to 0
    end
    pdf(ii, :) = pdf_1d;
end

odf_indirect = sum(pdf .* repmat(rs', [length(odf_dirs), 1]), 2);
odf_indirect(odf_indirect < 0) = 0; % clip negative values
odf_indirect = odf_indirect - min(odf_indirect(:)); % remove offset

% display odf
odf_actor = fvc;
odf_actor.vertices = fvc.vertices .* repmat(odf_indirect, [1, 3]); % scale radial distance
odf_actor.facevertexcdata = odf_indirect; % change color data to represent pdf values

figure
h = patch(odf_actor);
view(0, 0)
lighting gouraud
shading faceted
camlight
set(h, 'EdgeColor', 'none');

colormap;
colorbar;
caxis([min(odf_indirect(:)), max(odf_indirect(:))]);

axis equal, axis off, axis tight
title('indirect odf');

Published with MATLAB® R2018a